§ 1.Постановка задачи.

В силу особого вида тензора Римана пространства V_n в случае n=2, для метрического тензора ассоциированного пространства второго порядка двумерного риманова пространства получим выражение:

(1) ,

где , y_i -римановы нормальные координаты , выраженные ковариантными компонентами, - гауссова кривизна в начале координат.

Ставится вопрос нахождения поверхности в E₃ , для которой (1) будет выражать коэффициенты первой квадратичной формы, то есть, погружения двумерной метрики второго приближения в трёхмерное евклидово пространство. Отметим сразу, что реализацией метрики второго приближения нулевой кривизны является плоскость. Рассмотрим случаи ненулевой кривизны.

§ 2.Случай отрицательной кривизны.

Пусть задано некоторое число <0 . Рассмотрим поверхность в евклидовом пространстве, заданную в координатной форме формулами :

(2)

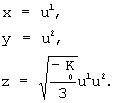
Матрица коэффициентов первой квадратичной формы рассматриваемой поверхности имеет вид:

(3) .

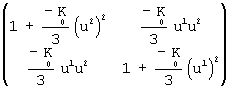Перейдём к новой системе координат на поверхности следующим образом:

(4)

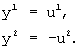
При этом коэффициенты первой квадратичной формы изменятся по закону:

(5) .

Учитывая то, что якобиан данного преобразования имеет вид:

получим матрицу коэффициентов новой первой квадратичной формы:

(6) .

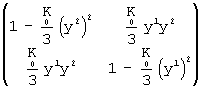Сравнение (1) и (6) приводит к выводу, что поверхность (2) реализует метрику второго приближения (1) отрицательной кривизны в трёхмерном евклидовом пространстве.

§ 3.Случай положительной кривизны.

Для погружения метрики второго приближения положительной кривизны воспользуемся методом Дарбу.Уравнение Дарбу для метрики (1) примет вид:

(7)

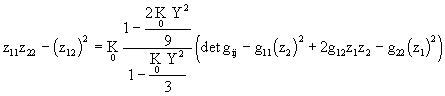
В дальнейшем будем рассматривать такую окрестность начала координат, что . В такой окрестности метрический тензор (1) будет невырожденным, а правая часть уравнения (7)- непрерывной функцией по переменным y¹ ,y^2.

Условие разрешимости уравнения (7), приведённое в [1], в сделанном предположении эквивалентно условию, следовательно уравнение(7) разрешимо.

Попытаемся найти решения уравнения (7) в предположении . В таком случае уравнение (7) примет вид:

(8) .

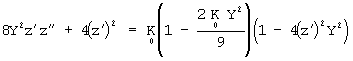Заменой неизвестной функции приведём (8) к линейному неоднородному дифференциальному уравнению первого порядка относительно функции v одной переменной Y^2:

(9) .

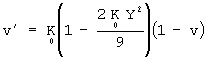Учитывая требование v(0)=0 , получим

,

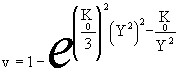откуда

(10) ,

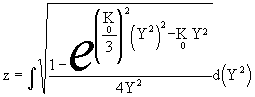причём .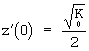

Перейдя к длине дуги как параметру, получим более простое выражение для z:

(11)

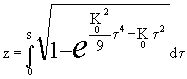
В [2] приводится теорема:

Пусть и - два обобщённых решения уравнения

,

совпадающих на границе области . Пусть , а F для любых и для любых конечных z, z₁ и z₂ такова, что

Она непрерывна и неотрицательна.

Как функция z при фиксированных значениях остальных аргументов она абсолютно непрерывна и

,

тогда и совпадают в тождественно.

Где - класс функций, выпуклых на W и C¹(W )- класс класс функций, непрерывных на W вместе с частными производными первого порядка.

В [5] указано, что эта теорема остаётся справедливой, если условие заменить условиями: и F удовлетворяет условию Липшица по z₁ и z_2.

При выборе 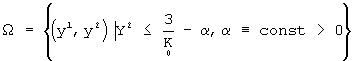все эти условия выполняются и функция (10) является единственным решением уравнения (8) в классе функций , где .

Условие F>0 эквивалентно при 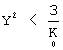условию , что является необходимым условием того, что z - решение уравнения Дарбу (7). Замечая, что F непрерывна по z₁ и z₂, можем утверждать, что в достаточно малой окрестности точки (0,0) функция (10)является единственным решением уравнения (7) в классе функций .

Воспользуемся тем фактом, что в рассматриваемой окрестности, по определению римановых нормальных координат, любая точка может быть соединена с началом координат при помощи геодезической единственным образом. Попытаемся найти реализацию данной метрики в виде поверхности вращения, полученной вращением некоторой кривой вокруг нормали к поверхности, построенной в начале координат. В данном случае этой единственной геодезической будет меридиан, проходящий через данную точку. Кривую зададим параметрически, отнесенной к каноническому параметру:

Здесь функция z(S) взята из (11), а x(S) можно найти из условия

Окончательно, параметрическое задание данной кривой примет вид:

(12)

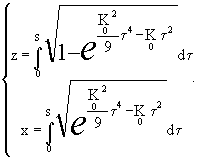
Литература:

1.Бакельман И.Я и др. Введение в дифференциальную геометрию “в целом”. М,1967.

2.Бакельман И.Я. Геометрические методы решения эллиптических уравнений. М,1969.

3.Бакельман И.Я. Высшая геометрия. М., “Просвещение”, 1967.

4. Погорелов А.В. Об уравнениях Монжа-Ампера эллиптического типа. ХГУ,1960.

5. Эйзенхарт Л.П. Риманова геометрия. М,Инлит.,1948.